Dimension 行數(shù)和列數(shù)DotProduct 點(diǎn)積BilinearForm 向量的雙線性形式EigenConditionNumbers 計(jì)算數(shù)值特征值制約問題的特征值或特征向量的條件數(shù)Eigenvalues 計(jì)算矩陣的特征值Eigenvectors 計(jì)算矩陣的特征向量Equal 比較兩個(gè)向量或矩陣是否相等ForwardSubstitute 求解 A . X = B，其中 A 為下三角型行階梯矩陣FrobeniusForm 將一個(gè)方陣約化為 Frobenius 型（有理標(biāo)準(zhǔn)型）GaussianElimination 對矩陣作高斯消元ReducedRowEchelonForm 對矩陣作高斯－約當(dāng)消元GetResultDataType 返回矩陣或向量運(yùn)算的結(jié)果數(shù)據(jù)類型在科學(xué)研究和工程技術(shù)中，科學(xué)計(jì)算軟件已成為不可或缺的工具。青浦區(qū)購買科學(xué)計(jì)算軟件供應(yīng)

三、科學(xué)計(jì)算軟件的發(fā)展趨勢隨著計(jì)算機(jī)技術(shù)的不斷發(fā)展，科學(xué)計(jì)算軟件也在不斷更新?lián)Q代。當(dāng)前，科學(xué)計(jì)算軟件的發(fā)展趨勢主要呈現(xiàn)以下幾個(gè)方面：云計(jì)算與大數(shù)據(jù)整合：云計(jì)算架構(gòu)的普及使得科學(xué)計(jì)算軟件能夠更加高效地利用計(jì)算資源，降低本地硬件的依賴。同時(shí)，大數(shù)據(jù)技術(shù)的整合使得軟件能夠處理更加復(fù)雜、龐大的數(shù)據(jù)集，提高計(jì)算的準(zhǔn)確性和效率。人工智能與機(jī)器學(xué)習(xí)集成：AI技術(shù)的集成使得科學(xué)計(jì)算軟件具備更強(qiáng)的自主決策能力。例如，通過自動(dòng)化測試、智能推薦等功能，軟件能夠輔助用戶更加高效地完成計(jì)算任務(wù)。青浦區(qū)購買科學(xué)計(jì)算軟件供應(yīng)它們提供了強(qiáng)大的數(shù)值計(jì)算能力和靈活的編程接口，可以滿足各種復(fù)雜的計(jì)算需求。

CharacteristicPolynomial 構(gòu)造矩陣的特征多項(xiàng)式CompanionMatrix 構(gòu)造一個(gè)首一（或非首一）多項(xiàng)式或矩陣多項(xiàng)式的友矩陣（束）ConditionNumber 計(jì)算矩陣關(guān)于某范數(shù)的條件數(shù)ConstantMatrix 構(gòu)造常數(shù)矩陣ConstantVector 構(gòu)造常數(shù)向量Copy 構(gòu)造矩陣或向量的一份復(fù)制CreatePermutation 將一個(gè) NAG 主元向量轉(zhuǎn)換為一個(gè)置換向量或矩陣CrossProduct 向量的叉積`&x` 向量的叉積DeleteRow 刪除矩陣的行DeleteColumn刪除矩陣的列Determinant 行列式Diagonal 返回從矩陣中得到的向量序列DiagonalMatrix 構(gòu)造（分塊）對角矩陣

1.4 素?cái)?shù)Randpoly, Randprime - 有限域的隨機(jī)多項(xiàng)式/首一素?cái)?shù)多項(xiàng)式ithprime - 確定第 i 個(gè)素?cái)?shù)nextprime, prevprime - 確定下一個(gè)比較大/**小素?cái)?shù)1.5 數(shù)的進(jìn)制轉(zhuǎn)換convert/base - 基數(shù)之間的轉(zhuǎn)換convert/binary - 轉(zhuǎn)換為二進(jìn)制形式convert/decimal - 轉(zhuǎn)換為 10 進(jìn)制convert/double - 將雙精度浮點(diǎn)數(shù)由一種形式轉(zhuǎn)換為另一種形式convert/float - 轉(zhuǎn)換為浮點(diǎn)數(shù)convert/hex - 轉(zhuǎn)換為十六進(jìn)制形式convert/metric - 轉(zhuǎn)換為公制單位convert/octal - 轉(zhuǎn)換為八進(jìn)制形式1.6 數(shù)的類型檢查type - 數(shù)的類型檢查函數(shù)第2章 初等數(shù)學(xué)2.1 初等函數(shù)product - 確定乘積求和不確定乘積它們提高了計(jì)算的準(zhǔn)確性和效率，還推動(dòng)了科學(xué)技術(shù)的進(jìn)步和發(fā)展。

★ 提供世界上**強(qiáng)大的符號計(jì)算和高性能數(shù)值計(jì)算引擎，包括世界上**強(qiáng)大的微分方程求解器（ODEs，PDEs，高指數(shù)DAEs）。★ 智能自動(dòng)算法選擇。★ 強(qiáng)大、靈活、容易使用的編程語言，讓您能夠開發(fā)更復(fù)雜的模型或算法。★ 與多學(xué)科復(fù)雜系統(tǒng)建模和仿真平臺(tái)MapleSim緊密集成。技術(shù)文件環(huán)境★ 大量易學(xué)易用的工具和特征，提供“數(shù)學(xué)版office”工作環(huán)境，用戶即使沒有任何語法知識(shí)也可以完成大量數(shù)學(xué)問題的計(jì)算，***地縮短學(xué)習(xí)時(shí)間。★技術(shù)文件界面組合文字、數(shù)學(xué)、圖形、聲音、建模、科學(xué)計(jì)算等您所有的工作。Octave：與MATLAB兼容的開源軟件，適合進(jìn)行數(shù)值計(jì)算和算法開發(fā)。楊浦區(qū)購買科學(xué)計(jì)算軟件推薦

這些軟件通常提供強(qiáng)大的數(shù)學(xué)庫和可視化功能，適用于工程、物理、化學(xué)、生物等多個(gè)領(lǐng)域。青浦區(qū)購買科學(xué)計(jì)算軟件供應(yīng)

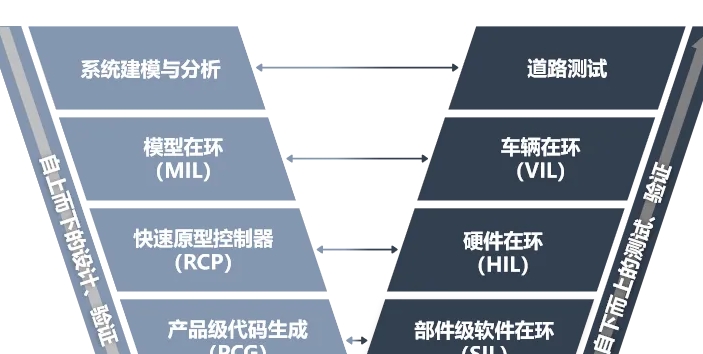
二、科學(xué)計(jì)算軟件的應(yīng)用科學(xué)計(jì)算軟件的應(yīng)用范圍廣泛，幾乎涵蓋了所有需要精確計(jì)算的領(lǐng)域。在高等教育中，科學(xué)計(jì)算軟件成為學(xué)生學(xué)習(xí)高等數(shù)學(xué)、物理、工程等學(xué)科的得力助手。例如，Matlab軟件在數(shù)列極限、函數(shù)極限教學(xué)中的應(yīng)用，極大地幫助學(xué)生理解和掌握這些抽象概念。在科研領(lǐng)域，科學(xué)計(jì)算軟件更是不可或缺。研究人員可以利用這些軟件進(jìn)行復(fù)雜的模擬實(shí)驗(yàn)、數(shù)據(jù)分析以及結(jié)果可視化，從而加速科研進(jìn)程，提高研究效率。此外，科學(xué)計(jì)算軟件還在工程設(shè)計(jì)、金融分析、醫(yī)學(xué)圖像處理等領(lǐng)域發(fā)揮著重要作用。在工程設(shè)計(jì)領(lǐng)域，工程師可以利用軟件進(jìn)行結(jié)構(gòu)分析、流體動(dòng)力學(xué)模擬等，以優(yōu)化設(shè)計(jì)方案，降**造成本。在金融分析領(lǐng)域，科學(xué)計(jì)算軟件能夠處理大量的市場數(shù)據(jù)，幫助投資者做出更加明智的決策。在醫(yī)學(xué)圖像處理領(lǐng)域，軟件能夠輔助醫(yī)生進(jìn)行病灶檢測、手術(shù)規(guī)劃等，提高醫(yī)療服務(wù)的質(zhì)量和效率。青浦區(qū)購買科學(xué)計(jì)算軟件供應(yīng)

甘茨軟件科技（上海）有限公司在同行業(yè)領(lǐng)域中，一直處在一個(gè)不斷銳意進(jìn)取，不斷制造創(chuàng)新的市場高度，多年以來致力于發(fā)展富有創(chuàng)新價(jià)值理念的產(chǎn)品標(biāo)準(zhǔn)，在上海市等地區(qū)的數(shù)碼、電腦中始終保持良好的商業(yè)口碑，成績讓我們喜悅，但不會(huì)讓我們止步，殘酷的市場磨煉了我們堅(jiān)強(qiáng)不屈的意志，和諧溫馨的工作環(huán)境，富有營養(yǎng)的公司土壤滋養(yǎng)著我們不斷開拓創(chuàng)新，勇于進(jìn)取的無限潛力，甘茨軟件供應(yīng)攜手大家一起走向共同輝煌的未來，回首過去，我們不會(huì)因?yàn)槿〉昧艘稽c(diǎn)點(diǎn)成績而沾沾自喜，相反的是面對競爭越來越激烈的市場氛圍，我們更要明確自己的不足，做好迎接新挑戰(zhàn)的準(zhǔn)備，要不畏困難，激流勇進(jìn)，以一個(gè)更嶄新的精神面貌迎接大家，共同走向輝煌回來！