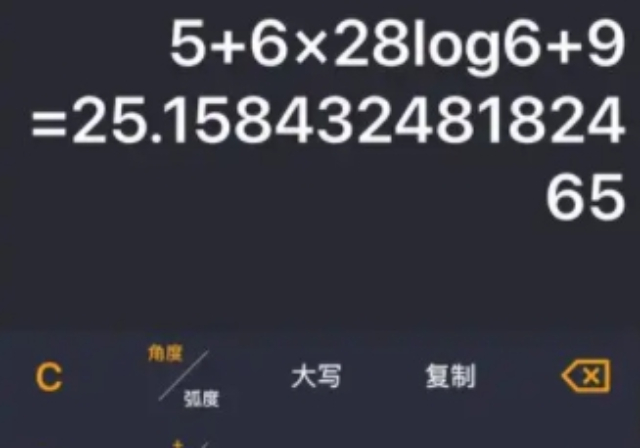
靜安區(qū)常見科學(xué)計(jì)算軟件設(shè)計(jì)
- 品牌
- 甘茨
- 服務(wù)項(xiàng)目
- 齊全
Octave是一種編程語言,旨在解決線性和非線性的數(shù)值計(jì)算問題。Octave為GNU項(xiàng)目下的開源軟件,早期版本為命令行交互方式,4.0.0版本發(fā)布基于QT編寫的GUI交互界面。Octave語法與Matlab語法非常接近,可以很容易的將matlab程序移植到Octave。同時(shí)與C++,QT等接口較Matlab更加方便。Octave是一種科學(xué)計(jì)算軟件,旨在提供與Matlab語法兼容的開放源代碼科學(xué)計(jì)算及數(shù)值分析的工具;它同時(shí)也是GNU項(xiàng)目成員之一。操作界面。 [1]系統(tǒng)性開發(fā)則是由John W. Eaton在1992年接手才開始的。 ***個(gè)alpha測試版是在1993年1月4日發(fā)布,1.0穩(wěn)定版則是在1994年2月17日發(fā)布。它們提供了強(qiáng)大的數(shù)值計(jì)算能力和靈活的編程接口,可以滿足各種復(fù)雜的計(jì)算需求。靜安區(qū)常見科學(xué)計(jì)算軟件設(shè)計(jì)
Dimension 行數(shù)和列數(shù)DotProduct 點(diǎn)積BilinearForm 向量的雙線性形式EigenConditionNumbers 計(jì)算數(shù)值特征值制約問題的特征值或特征向量的條件數(shù)Eigenvalues 計(jì)算矩陣的特征值Eigenvectors 計(jì)算矩陣的特征向量Equal 比較兩個(gè)向量或矩陣是否相等ForwardSubstitute 求解 A . X = B,其中 A 為下三角型行階梯矩陣FrobeniusForm 將一個(gè)方陣約化為 Frobenius 型(有理標(biāo)準(zhǔn)型)GaussianElimination 對矩陣作高斯消元ReducedRowEchelonForm 對矩陣作高斯-約當(dāng)消元GetResultDataType 返回矩陣或向量運(yùn)算的結(jié)果數(shù)據(jù)類型楊浦區(qū)智能科學(xué)計(jì)算軟件24小時(shí)服務(wù)它們提高了計(jì)算的準(zhǔn)確性和效率,還推動(dòng)了科學(xué)技術(shù)的進(jìn)步和發(fā)展。
CharacteristicPolynomial 構(gòu)造矩陣的特征多項(xiàng)式CompanionMatrix 構(gòu)造一個(gè)首一(或非首一)多項(xiàng)式或矩陣多項(xiàng)式的友矩陣(束)ConditionNumber 計(jì)算矩陣關(guān)于某范數(shù)的條件數(shù)ConstantMatrix 構(gòu)造常數(shù)矩陣ConstantVector 構(gòu)造常數(shù)向量Copy 構(gòu)造矩陣或向量的一份復(fù)制CreatePermutation 將一個(gè) NAG 主元向量轉(zhuǎn)換為一個(gè)置換向量或矩陣CrossProduct 向量的叉積`&x` 向量的叉積DeleteRow 刪除矩陣的行DeleteColumn刪除矩陣的列Determinant 行列式Diagonal 返回從矩陣中得到的向量序列DiagonalMatrix 構(gòu)造(分塊)對角矩陣
Beta - Beta函數(shù)EllipticModulus - 模數(shù)函數(shù)k(q)GAMMA, lnGAMMA - 完全和不完全Gamma函數(shù)GaussAGM - Gauss 算術(shù)的幾何平均數(shù)JacobiAM, ., - Jacobi 振幅函數(shù)和橢圓函數(shù)JacobiTheta1, JacobiTheta4 - Jacobi theta函數(shù)JacobiZeta - Jacobi 的Zeta函數(shù)KelvinBer, KelvinBei - Kelvin函數(shù)KummerM, - Kummer M函數(shù)和U函數(shù)LambertW - LambertW函數(shù)LerchPhi - 一般的Lerch Phi函數(shù)LommelS1, LommelS2 - Lommel函數(shù)MeijerG - 一個(gè)修正的Meijer G函數(shù)Psi - Digamma 和Polygamma函數(shù)StruveH, StruveL - Struve函數(shù)WeierstrassP - Weierstrass P函數(shù)及其導(dǎo)數(shù)研究人員可以利用這些軟件進(jìn)行復(fù)雜的模擬實(shí)驗(yàn)、數(shù)據(jù)分析以及結(jié)果可視化,從而加速科研進(jìn)程,提高研究效率。

student[changevar] - 變量代換dawson - Dawson 積分ellipsoid - 橢球體的表面積evalf(int) - 數(shù)值積分intat, Intat - 在一個(gè)點(diǎn)上積分求值第10章 微分方程10.1 微分方程分類odeadvisor - ODE-求解分析器DESol - 表示微分方程解的數(shù)據(jù)結(jié)構(gòu)pdetest - 測試pdsolve 能找到的偏微分方程(PDEs)解10.2 常微分方程求解solve - 求解常微方程 (ODE)dsolve - 用給定的初始條件求解ODE 問題dsolve/inttrans - 用積分變換方法求解常微分方程dsolve/numeric - 常微方程數(shù)值解dsolve/piecewise - 帶分段系數(shù)的常微方程求解dsolve - 尋找ODE 問題的級數(shù)解在科研領(lǐng)域,科學(xué)計(jì)算軟件更是不可或缺。金山區(qū)怎樣科學(xué)計(jì)算軟件設(shè)計(jì)
學(xué)計(jì)算軟件還在工程設(shè)計(jì)、金融分析、醫(yī)學(xué)圖像處理等領(lǐng)域發(fā)揮著重要作用。靜安區(qū)常見科學(xué)計(jì)算軟件設(shè)計(jì)
QRDecomposition QR 分解RandomMatrix 構(gòu)造隨機(jī)矩陣RandomVector 構(gòu)造隨機(jī)向量Rank 計(jì)算矩陣的秩Row 返回矩陣的一個(gè)行向量序列Column 返回矩陣的一個(gè)列向量序列RowOperation 對矩陣作初等行變換ColumnOperation 對矩陣作出等列變換RowSpace 返回矩陣行空間的一組基ColumnSpace 返回矩陣列空間的一組基ScalarMatrix 構(gòu)造一個(gè)單位矩陣的數(shù)量倍數(shù)ScalarVector 構(gòu)造一個(gè)單位向量的數(shù)量倍數(shù)ScalarMultiply 矩陣與數(shù)的乘積MatrixScalarMultiply 計(jì)算矩陣與數(shù)的乘積VectorScalarMultiply 計(jì)算向量與數(shù)的乘積靜安區(qū)常見科學(xué)計(jì)算軟件設(shè)計(jì)
甘茨軟件科技(上海)有限公司是一家有著雄厚實(shí)力背景、信譽(yù)可靠、勵(lì)精圖治、展望未來、有夢想有目標(biāo),有組織有體系的公司,堅(jiān)持于帶領(lǐng)員工在未來的道路上大放光明,攜手共畫藍(lán)圖,在上海市等地區(qū)的數(shù)碼、電腦行業(yè)中積累了大批忠誠的客戶粉絲源,也收獲了良好的用戶口碑,為公司的發(fā)展奠定的良好的行業(yè)基礎(chǔ),也希望未來公司能成為*****,努力為行業(yè)領(lǐng)域的發(fā)展奉獻(xiàn)出自己的一份力量,我們相信精益求精的工作態(tài)度和不斷的完善創(chuàng)新理念以及自強(qiáng)不息,斗志昂揚(yáng)的的企業(yè)精神將**甘茨軟件供應(yīng)和您一起攜手步入輝煌,共創(chuàng)佳績,一直以來,公司貫徹執(zhí)行科學(xué)管理、創(chuàng)新發(fā)展、誠實(shí)守信的方針,員工精誠努力,協(xié)同奮取,以品質(zhì)、服務(wù)來贏得市場,我們一直在路上!
expand -表達(dá)式展開Expand - 展開表達(dá)式的惰性形式expandoff/expandon - 抑制/不抑制函數(shù)展開5.2 因式分解Afactor - ***因式分解的惰性形式Afactors - ***因式分解分解項(xiàng)列表的惰性形式Berlekamp - 因式分解的Berlekamp 顯式度factor - 多元的多項(xiàng)式的因式分解factors - 多元多項(xiàng)式的因式分解列表Factor - 函數(shù)factor 的惰性形式Factors - 函數(shù)factors 的惰性形式polytools[splits] - 多項(xiàng)式的完全因式分解第6章 化簡6.1 表達(dá)式化簡118simplify - ...
- 青浦區(qū)特色科學(xué)計(jì)算軟件比較 2025-07-15
- 徐匯區(qū)質(zhì)量科學(xué)計(jì)算軟件價(jià)格 2025-07-15
- 奉賢區(qū)質(zhì)量科學(xué)計(jì)算軟件圖片 2025-07-15
- 長寧區(qū)質(zhì)量科學(xué)計(jì)算軟件服務(wù)電話 2025-07-15
- 嘉定區(qū)常見科學(xué)計(jì)算軟件推薦 2025-07-14
- 黃浦區(qū)特色科學(xué)計(jì)算軟件服務(wù)電話 2025-07-14
- 上海品牌科學(xué)計(jì)算軟件24小時(shí)服務(wù) 2025-07-14
- 閔行區(qū)購買科學(xué)計(jì)算軟件比較 2025-07-13
- 寶山區(qū)怎樣科學(xué)計(jì)算軟件推薦 2025-07-13
- 楊浦區(qū)購買科學(xué)計(jì)算軟件推薦 2025-07-13
- 嘉定區(qū)挑選科學(xué)計(jì)算軟件供應(yīng) 2025-07-11
- 青浦區(qū)特色科學(xué)計(jì)算軟件價(jià)格 2025-07-11
- 青浦區(qū)質(zhì)量科學(xué)計(jì)算軟件比較 2025-07-10
- 徐匯區(qū)質(zhì)量科學(xué)計(jì)算軟件供應(yīng) 2025-07-09
- 上海特色科學(xué)計(jì)算軟件供應(yīng) 2025-07-09
- 閔行區(qū)怎樣科學(xué)計(jì)算軟件推薦 2025-07-09


- 奉賢區(qū)質(zhì)量Matlab比較 07-15
- 青浦區(qū)特色科學(xué)計(jì)算軟件比較 07-15
- 徐匯區(qū)質(zhì)量科學(xué)計(jì)算軟件價(jià)格 07-15
- 奉賢區(qū)質(zhì)量科學(xué)計(jì)算軟件圖片 07-15
- 長寧區(qū)質(zhì)量科學(xué)計(jì)算軟件服務(wù)電話 07-15
- 嘉定區(qū)常見科學(xué)計(jì)算軟件推薦 07-14
- 黃浦區(qū)特色科學(xué)計(jì)算軟件服務(wù)電話 07-14
- 金山區(qū)挑選系統(tǒng)建模軟件設(shè)計(jì) 07-14
- 青浦區(qū)挑選AUTOSAR工具鏈比較 07-14
- 普陀區(qū)購買AUTOSAR工具鏈比較 07-14